Ну що, спробували розв'язати головоломку Льюїса Керролла. Деякі з вас впроралися швидко, а хтось не розв'язав зовсім. Чому це відбувається? Як правильно малювати, щоб вийшло? Щоб відповісти на ці питання, звернемося до математики.

Головоломка "Сім кенігсберзьких мостів" у 1735 році стала відома математику Леонарду Ейлеру. Ейлер довів, що ця задача не має розв'язку. Звичайно, Ейлер вирішив не тільки завдання про кенігсбергські мости, а цілий клас схожих завдань, для яких розробив метод вирішення. У наш час схема з точок і ліній, якою Ейлер замінив мости, називається графом, точки називають вершинами графа, а лінії - ребрами графа.

У кожній вершині графа сходиться кілька ліній. Якщо число ліній парне, то вершина називається парна, якщо число ліній непарна, то вершина називається непарною.

Питання можливості накреслення головоломки одним розчерком олівця зводиться до побудови графа у теорії Ейлера. Є декілька правил щодо побудови:

1. Якщо в графі немає непарних точок, то зображення можна намалювати одним розчерком, не відриваючи олівця від паперу, починаючи з будь-якого місця.
2. Якщо в графі дві непарні вершини, то зображення можна накреслити одним розчерком, не відриваючи олівця від паперу, причому креслити потрібно починати в одній непарної точці, а закінчити в інший.
3. Якщо в графі більше двох непарних вершин, то зображення не можна накреслити одним розчерком олівця.

Давайте розглянемо задачу побудови розгорнутого конверта не відриваючи руки.

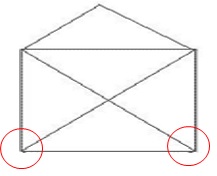
Дві вершини конверта непарні, тому використовуючи правило Ейлера ми можемо намалювати конверт не відриваючи руки. Пам'ятаємо правило - починати треба з однієї непарної вершини, і закінчувати у другій. Розглянемо одне з рішень

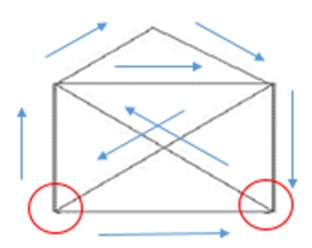
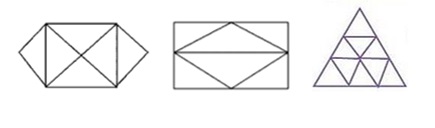
Спробуйте розв'язати головоломки запропоновані нижче

До Ейлера ні кому в голову не приходило, що головоломка про мости та інші головоломки з обходом контуру, має відношення до математики. Аналіз Ейлера таких завдань є першим паростком галузі математики, сьогодні відомої під назвою топологія.